摘要：微分符号代表了微小的变化量，是数学分析中的重要概念。dx与dy则是微分表达式中的微分元，表示自变量和因变量的微小变化。它们背后真正的含义是描述函数在某一点的局部变化率，广泛应用于物理、工程、经济等领域。通过微分，可以更加深入地理解函数的性质和行为。

本文目录导读：

1. 微分符号
2. dx和dy的含义
3. 微分符号、dx和dy的关系

当我们谈论微积分时，我们经常会遇到一些看似神秘却又极其重要的概念，如微分符号、dx和dy，这些概念对于理解微积分的基本原理至关重要，本文将深入探讨它们的含义和背后的理念。

微分符号

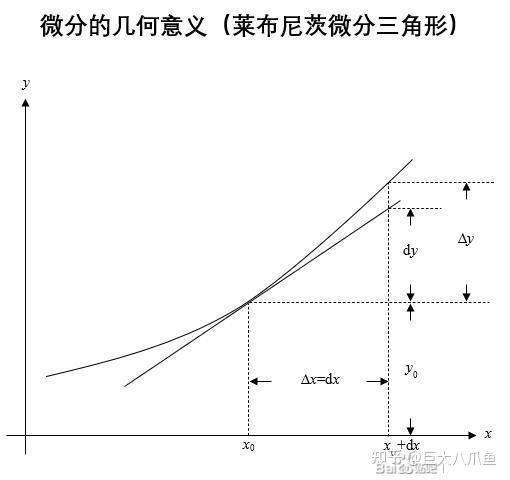
微分符号"d"是一个表示微小变化或无穷小变化的标记，在微积分中，当我们谈论一个函数在某一点的导数时，我们实际上是在讨论该函数在该点的微小变化率，微分符号帮助我们量化这种微小的变化，使我们能够精确地理解函数的变化行为，如果我们有一个函数y = f(x)，那么我们可以使用微分符号来表示y关于x的微小变化，即dy/dx，这里的dy表示函数y的微小变化量，而dx则表示自变量x的微小变化量，这种表达方式为我们提供了一种量化函数局部行为的方法。

dx和dy的含义

当我们谈论dx和dy时，我们实际上是在谈论函数的自变量和因变量的微小变化量，dx表示自变量x的微小变化量，而dy表示因变量y随着x变化而发生的微小变化量，在微积分中，这些微小的变化量帮助我们理解函数的局部行为，特别是函数的斜率（即导数），通过计算dy/dx，我们可以得到函数在某一特定点的斜率，这个斜率表示了函数在该点的切线斜率，dx和dy为我们提供了一种量化函数局部斜率的方法。

微分符号、dx和dy的关系

微分符号、dx和dy之间的关系密切且相互依赖，微分符号帮助我们表示函数的微小变化量，而dx和dy则具体描述了这些微小变化量的数值，通过计算dy/dx，我们可以得到函数在某一点的导数，这个导数描述了函数在该点的斜率或变化率，这种关系使我们能够精确地理解函数的局部行为，从而进行更深入的数学分析。

为了更好地理解这些概念，我们可以考虑一个简单的例子：一个物体在直线上的运动，假设物体的位置是时间t的函数s(t)，在这个情况下，ds/dt表示物体在任意时刻的速度，即位置随时间的变化率，这里的ds是物体位置的微小变化量（即dy），而dt是时间的微小变化量（即dx），ds/dt为我们提供了物体在任意时刻的速度，帮助我们理解物体的运动行为。

微分符号、dx和dy是微积分中非常重要的概念，它们帮助我们量化函数的微小变化量，从而理解函数的局部行为，通过理解这些概念，我们可以更深入地理解微积分的基本原理，包括导数和积分，这些概念的应用范围非常广泛，包括物理、工程、经济学和其他许多领域，掌握这些概念对于理解和应用微积分至关重要。

通过本文的探讨，我们了解到微分符号表示的是微小变化或无穷小变化的标记，而dx和dy则具体描述了函数的自变量和因变量的微小变化量，这些概念之间的关系密切且相互依赖，使我们能够精确地理解函数的局部行为，希望本文能够帮助读者更好地理解这些重要的微积分概念，为未来的学习和应用打下坚实的基础。