摘要:葛立恒数的平方是否大于原数,这个问题涉及到巨大的数值比较。葛立恒数是一个极其庞大的数,其平方意味着每个位数都要与自己相乘,结果将是一个更为巨大的数。但目前无法确定其平方是否远远大于原数,因为这需要具体的数值计算或证明,远远超出常规数学范畴。
本文目录导读:
当我们谈及葛立恒数时,我们不得不提及这个巨大的数学概念所带来的震撼,葛立恒数,作为一个令人难以置信的巨大数,其定义和特性已经引起了众多数学家和数学爱好者的关注,当我们谈论葛立恒数的平方时,是否意味着这个数值远远超过了葛立恒数本身呢?让我们深入探讨这个问题。
葛立恒数的概念及其背景
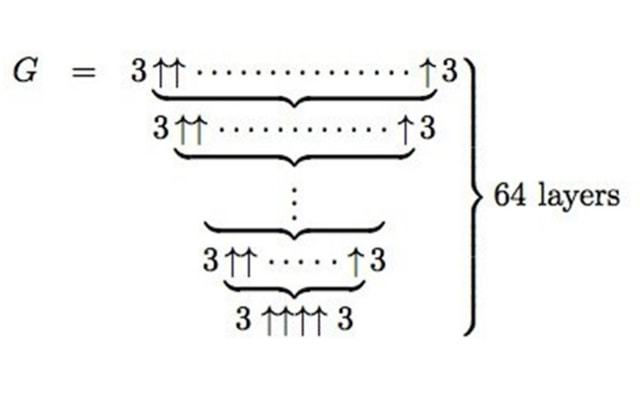
葛立恒数(Grahams number)是由美国计算机科学家罗纳德·葛立恒在1970年代提出的数学概念,它是一个巨大的数,通常用于描述某些数学问题中的极端大小,葛立恒数的定义涉及到一种特殊的符号系统,它代表了庞大的数学表达式中的嵌套和迭代运算,这个数主要用于解决某些特定的数学问题,尤其是与计算复杂性相关的领域。
葛立恒数的平方概念及其意义
当我们谈论葛立恒数的平方时,我们实际上是在讨论一个巨大的数值乘以自身的过程,这意味着我们将每个数字在原始数值中的位置相乘,形成一个新的数值,这个过程会导致结果迅速增长,远远超过了原始数值的大小,从直观上看,我们可以推测葛立恒数的平方应该是一个远远大于葛立恒数的数值。
数学证明与解析
为了证明这一点,我们需要深入理解数学中的指数运算规则,指数运算是一种强大的工具,用于描述重复乘法的过程,当我们将一个数进行平方时,实际上是将这个数乘以它自己,即该数的指数是2,这意味着平方操作会导致数值迅速增长,对于任何正实数来说,其平方都会大于其本身,我们可以得出结论:葛立恒数的平方确实是一个远远大于葛立恒数的数值。
葛立恒数在实际应用中的意义
尽管葛立恒数看起来非常庞大且遥不可及,但它在实际应用中具有一定的意义,在计算机科学领域,葛立恒数被用于描述某些算法的计算复杂性,它还在一些数学领域中用于解决特定的数学问题,尽管我们无法在现实生活中真正使用到如此庞大的数值,但研究这些巨大的数学概念有助于我们更深入地理解数学的本质和计算复杂性。
我们可以确定地得出结论:葛立恒数的平方确实是一个远远大于葛立恒数的数值,这一结论揭示了指数运算的强大之处以及数学中的巨大数值可以如何迅速增长,通过研究这些巨大的数学概念,我们可以更深入地理解数学的本质和计算复杂性,我们还可以从中学到一种重要的思维方式,即通过抽象和符号系统来处理极端大小的数值,这种思维方式有助于我们解决现实生活中的复杂问题,推动科学和技术的进步。
葛立恒数的平方是否远远大于葛立恒数这一问题引发了我们对数学中巨大数值和指数运算的深入思考,通过深入探讨这一概念,我们不仅可以更好地理解数学的本质和计算复杂性,还可以将这种思维方式应用于现实生活中的问题,推动科学和技术的不断发展。

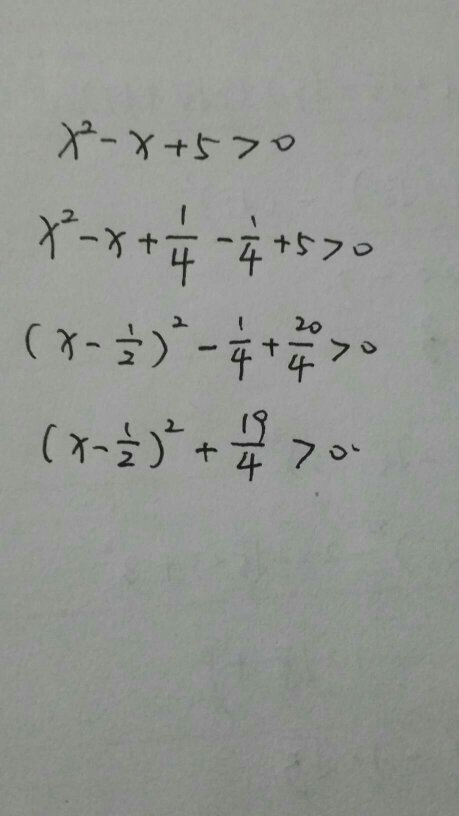

 京ICP备11000001号
京ICP备11000001号